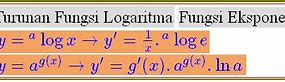
Contoh Soal Logaritma
Berikut adalah salah satu contoh soal logaritma, antara lain.
Pembahasannya Guna mengerjakan soal tersebut Anda perlu untuk memahami akan 3 (tiga) sifat logaritma, antara lain:
Setelah Anda memahami 3 (tiga) sifat diatas, maka Anda bisa memakai ketiga sifat itu guna menyelesaikan soal logaritma diatas.
Pertama Anda bisa memakai sifat pertama dan sifat kedua guna menyederhanakan pembilang dan juga penyebut pada soal logaritma tersebut.
Lalu, Anda akan memperoleh bentuk seperti diatas, kemudian Anda bisa memakai sifat ketiga guna menyederhanakan kembali menjadi bentuk seperti di bawah ini.
Anda bisa memakai penyederhanaan dengan bentuk log 10000 menjadi log 4.
Hasil dari penyelesaian soal logaritma tersebut yaitu ¼.
Bagi Anda yang belum mengetahui atau belum mempelajari tentang eksponensial atau bisa disebut juga dengan perpangkatan. Maka Anda perlu mengetahuinya secara lebih dalam lagi. Lalu, Apa saja yang bisa Anda pelajari dan pahami dari materi eksponensial ini?
Konsep materi dari eksponensial yang akan dipakai pada pembahasan kali ini yaitu mempelajari materi dari logaritma. Materi logaritma ini sangat penting Anda ketahuinya, agar Anda dapat mengetahui manfaat dari logaritma dalam kehidupan sehari-hari. Nah, Apa saja itu? Mari perhatikan pembahasan berikut ini mulai dari pengertian logaritma hingga contoh soal.
Mengetahui sifat dari logaritma, di dalam suatu ilmu matematika, logaritma adalah kebalikan atau invers dari eksponen atau pemangkatan. Secara sederhananya saja, logaritma bisa diartikan sebagai suatu invers atau kebalikan dari pemangkatan yang digunakan dalam menentukan besaran pangkat pada sebuah bilangan pokok.
Sehingga intinya bahwa dengan Anda mempelajari ilmu logaritma, maka Anda akan bisa mencari besaran pangkat dari suatu bilangan yang telah diketahui hasil pangkatnya.
Fungsi logaritma ini tidak cuma dipakai di dalam sebuah ilmu matematika saja, akan tetapi juga dipakai di dalam ilmu pengetahuan alam atau biasa dikenal dengan sebutan IPA. Serta juga digunakan pada ilmu kimia guna menentukan orde reaksi, pengetahuan akan akustik guna memilih koefisien serap bunyi yang pas, dan lain sebagainya. Selain itu, logaritma ini juga dipakai dalam mengukur laju pertumbuhan dari penduduk, antropologi dan keuangan guna menghitung bunga majemuk.
Logaritma Pada Kehidupan Sehari-Hari
Logaritma banyak dimanfaatkan dalam sebuah kehidupan sehari-hari. Dahulu, sebelum masyarakat mengenal adanya kalkulator, logaritma dimanfaatkan untuk menghitung perhitungan eksponensial.
Selain itu, ada manfaat lain dalam konsep logaritma ini. Konsep logaritma tersebut dipakai untuk melakukan perhitungan seismograf maupun alat pengukur kekuatan gempa.
Satuan skala richter ini juga memakai konsep logaritma di dalam perhitungannya. Dalam bidang astronomi juga dipakai sebagai alat perhitungan dalam mengukur tingkat keterangan dari suatu bintang. Nah, bagi Anda yang penasaran, bagaimana rumus logaritma. Berikut telah disajikan informasi terkait rumus logaritma.
Pada pembahasan sebelumnya Anda telah mengetahui pengertian dari logaritma dan manfaat dari logaritma. Berikut merupakan pembahasan terkait rumus logaritma, diantaranya:
● Bentuk dari logaritma yang telah dinyatakan ke dalam bentuk alog b = c. ● Simbol a menyatakan suatu bilangan pokok logaritma maupun basis, b dengan menentukan range atau hasil dari logarigma, dan c adalah domain logaritma.
Setelah Anda mengetahui tentang rumus logaritma, Anda juga perlu mengetahui sifat logaritma.
Logaritma juga mempunyai sifat yang beraneka macam, nantinya sifat-sifat ini pula akan dapat membantu Anda dalam menyelesaikan soal-soal terkait logaritma. Cara yang dapat Anda lakukan yaitu mengetahui sifat logaritma, diantaranya sebagai berikut:
● Sifat logaritma dasar, yakni suatu bilangan yang dipangkatkan dengan angka 1, maka hasilnya akan tetap sama seperti yang sebelumnya. ● Sifat logaritma koefisien, yakni saat terdapat contoh terkait soal logaritma yang diberikan mempunyai pangkat. Maka pangkat dari basis atau biasa disebut numerus sebagai koefisien dari logaritma. ● Sifat logaritma akan berbanding terbalik, yakni suatu sifat yang mempunyai prasyarat berupa logaritma yang berbanding terbalik antara basis terhadap numerus. ● Sifat perpangkatan logaritma, adalah suatu bilangan yang dipangkatkan dengan logaritma yang mempunyai basis sama, maka hasilnya akan berupa suatu numerus dari logaritma itu sendiri. ● Sifat Penjumlahan dan pengurangan merupakan logaritma yang dapat dijumlahkan dengan logaritma lainnya yang mempunyai basis yang serupa. ● Sifat perkalian dan juga pembagian logaritma, adalah dua buah logaritma yang disederhanakan. Sebab keduanya mempunyai numerus yang serupa. ● Sifat logaritma numerus terbalik, maka logaritma bisa mempunyai nilai yang serupa dengan logaritma lainnya. Bila numerus menggunakan pecahan terbalik.
Selain itu, terdapat sejumlah sifat logaritma lainnya, yang penting untuk Anda ketahuinya, diantaranya:
● a log a = 1 ● a log 1 = 0 ● a^nlog bm = (m/n) x a log b ● a^mlog bm = a log b ● a log b = 1/b log a ● a log b = (klog b) / (klog a) ● a(a log b) = b ● a log b + a log c = a log (bc) ● a log b – a log c = a log (b/c) ● a log b . b log c = a log c ● a log (b/c) = – a log (c/b)
Selanjutnya terdapat pembahasan terkait persamaan logaritma. Mari perhatikan secara seksama.
Secara umum logaritma mempunyai sejumlah teknik penyelesaian yang mencakup persamaan logaritma, pertidaksamaan logaritma, dan juga cara menghitung logaritma. Berikut adalah pembahasannya.
Sifat Logaritma Numerus Terbalik
Sifat logaritma numerus terbalik ini merupakan logaritma yang memiliki nilai sama dengan logaritma yang lain. Hal ini dapat terjadi apabila numerus dan pecahan terbalik.
Setelah memahami pengertian logaritma dan penerapannya, rumus logaritma, sifat logaritma perlu pula memahami persamaan logaritma. Berikut ini pembahasan mengenai persamaan logaritma.
Contohnya, jika terdapat soal berupa alog f(x) dan alog g(x), maka kedua bentuk tersebut dapat dikatakan sama atau a log f(x) = alog g(x) jika f(x) = g(x) dengan syarat yakni a 1, a > 0, f(x) > 0, dan g(x) > 0.
Hafalan Rumus Matematika SMA/MA Kelas 10 11 12
Matematika merupakan mata pelajaran wajib yang diajarkan di tingkat dasar hingga menengah, hal tersebut sudah berlaku karena terdapat di dalam kurikulum yang dibuat oleh dinas terkait. Tidak sedikit dari murid yang mengaku tidak suka dengan pelajaran ini dengan berbagai alasan, mulai dari membosankan, guru yang killer, dsb.
Disiplin-disiplin utama di dalam matematika pertama muncul karena kebutuhan akan perhitungan di dalam perdagangan, untuk memahami hubungan antar bilangan, untuk mengukur tanah, dan untuk meramal peristiwa astronomi. Empat kebutuhan ini secara kasar dapat dikaitkan dengan pembagian-pembagian kasar matematika ke dalam pengkajian besaran, struktur, ruang, dan perubahan (yakni aritmatika, aljabar, geometri, dan analisis).
Buku Hafalan Rumus Matematika SMA/MA Kelas 10, 11, dan 12 hadir sebagai solusi bagi para siswa untuk menguasai keempat kajian matematika tersebut. Buku ini berisi kumpulan rumus dan ringkasan materi yang dilengkapi dengan contoh soal dan pembahasannya.
Disajikan dalam ukuran praktis agar dapat dipelajari kapan saja dan di mana saja. Buku ini bisa dijadikan pedoman yang berisi mengenai kumpulan rumus terlengkap dari mata pelajaran Matematika. Bentuknya yang praktis dan mudah dibawa-dibawa sangat cocok untuk menemani para siswa yang ingin mempelajarinya.
Tidak harus di dalam kelas, di manapun berada siswa bisa belajar dengan buku yang ringkas sekali tetapi isinya sangat kaya akan rumus-rumus praktis yang mudah diingat. Dengan satu buku ini sudah cukup membantu kamu semua untuk mendapatkan hasil maksimal di seluruh ulangan danuUjian di kelasmu. Karena buku ini berisi kumpulan rumus praktis matematika, ringkasan materi yang sudah terupdate, dan ratusan contoh soal-soal dan pembahasan.
● Pertidaksamaan Logaritma
Cara pertama guna menyelesaikan pertidaksamaan logaritma ini yaitu dengan menyamakan suatu bilangan pokoknya. Setelah itu, Anda perlu untuk mengikuti beberapa cara dibawah ini, antara lain:
● a log f(x) ≥ a log g(x)
Untuk bilangan pokok 0 < a < 1 f(x) ≤ g(x) f(x) > 0 g(x) > 0
Untuk bilangan pokok a>1
f(x) ≥ g(x) f(x) > 0 g(x) > 0
Semalam Suntuk Belajar Matematika SMA
Belajar Matematika nggak akan seru tanpa menghafal rumus, dan menghafal tidak akan lengkap tanpa sebuah buku yang isinya merangkum semua hal. Sebagian orang tidak mau mempelajari Matematika karena memang materinya yang banyak, rumus-rumusnya yang beragam dan tidak praktis seperti mata pelajaran yang lain. Sulitnya memahami pelajaran ini menjadi salah satu alasan banyak siswa membencinya.
Untuk mengatasi masalah tersebut, Anak Hebat Indonesia menerbitkan buku Semalam Suntuk Belajar Matematika SMA pada tahun 2018. Dengan tebal 272 halaman dengan ukuran 11 x 18 cm, buku ini dibuat kecil sehingga pas dalam genggaman kamu agar praktis dibawa kemanapun.
Buku yang disusun oleh Anastasia Angelica ini juga dikelompokkan dalam pokok-pokok bahasan yang gampang dimengerti dan disarikan langsung inti-intinya saja sehingga menjadi efektif dan efisien agar kalian para pembaca tidak pusing menghafalkan terlalu banyak materi. Penyampaiannya yang berbeda dari buku pelajaran pada umumnya menjadikan buku ini lebih menarik untuk para pelajar.
Buku yang dikhususkan untuk pelajar tingkat SMA ini dijamin akan membuat pelajar menguasai pelajaran Matematika dalam waktu singkat. Sesuai judulnya, dalam semalam setelah membaca dan memahami buku ini, kalian bisa langsung jadi ahli Matematika dan langsung bisa membabat habis semua soal Matematika yang muncul di ujian-ujian sekolah dengan mudah. Semoga dengan kehadiran buku ini kalian bisa menjadi ranking satu di sekolah!
● Persamaan Logaritma
Menyelesaikan persamaan logaritma dengan cara menyamakan suatu bilangan pokoknya. Berikut adalah teknik menghitungnya, antara lain: » a log f(x) = 8 log g(x), Caranya yaitu: f(x) = g(x) f(x) > 0 g(x) > 0
Sifat Logaritma Berbanding Terbalik
Sifat logaritma yang berikutnya adalah berbanding terbalik. Sifat ini merupakan sifat berprasyarat. Logaritma ini berbanding terbalik antara basis dan numerusnya.
Pertidaksamaan Logaritma
Selain itu, terdapat pula pertidaksamaan logaritma. Berikut ini contoh dan penyelesaiannya.
Contohnya, terdapat logaritma berupa alog f(x) dan alog g(x), maka dari kedua bentuk itu alog f(x) > alog g(x) jika a > 0 maka f(x) > g(x). Kemudian, 0 < a< 1 maka f(x) < g(x).
Setelah pembahasan mengenai pengertian logaritma, rumus logaritma, hingga persamaan dan pertidaksamaan logaritma, selanjutnya terdapat tabel logaritma. Tabel logaritma digunakan untuk mempermudah perhitungan nilai logaritma.
Cara menggunakan tabel logaritma yakni menentukan angka yang sesuai di bagian kolom paling kiri dan baris paling atas. Kemudian, cari nilai logaritma tersebut sesuai dengan baris dan kolom.
Demikian penjelasan terkait logaritma, mulai dari pengertian, rumus logaritma, sifat, persamaan, pertidaksamaan, dan tabel logaritma.
Pada artikel Matematika kelas 10 kali ini, kamu akan mempelajari tentang logaritma, sifat-sifat logaritma, dan contohnya. Yuk, simak artikelnya berikut ini!
Pada pembahasan sebelumnya, kamu telah mempelajari tentang dasar-dasar bilangan berpangkat (eksponen). Tentunya setelah itu, kamu jadi paham dan mahir dong ya dalam menentukan hasil dari suatu bilangan yang dipangkatkan.
Nah, materi yang akan kita bahas kali ini adalah kebalikan dari materi eksponen yang sebelumnya telah kamu pelajari. Apakah itu? Yap! Logaritma. Jadi, kalau di eksponen kamu disuruh mencari hasil pangkat, maka di logaritma kamu akan menentukan besar pangkat.
TIIDAAAAAXXX…!!! (Sumber: giphy.com)
Eits, tenang dulu. Materi ini tidak sesulit seperti yang kamu pikirkan, kok. Artikel ini akan membantu kamu untuk memahami logaritma dengan cara yang lebih mudah. So, daripada semakin penasaran, langsung saja yuk, kita simak pembahasannya bersama-sama!
Baca Juga: Cara Menyusun Persamaan dari Grafik Fungsi Kuadrat
Sebelumnya, mari kita ketahui dulu apa itu logaritma. Logaritma adalah suatu invers atau kebalikan dari pemangkatan (eksponen) yang digunakan untuk menentukan besar pangkat dari suatu bilangan pokok.
Jadi intinya, dengan mempelajari logaritma, kita bisa mencari besar pangkat dari suatu bilangan yang diketahui hasil pangkatnya.
“Loh, bukannya mencari besar pangkat itu mudah, ya? Misalnya, 2 pangkat berapa yang hasilnya 8, jawabannya pasti 3. Kenapa harus pusing-pusing belajar logaritma?”
Yeee… kalau itu sih memang mudah karena bilangan yang memiliki pangkat dan bilangan hasil pemangkatannya itu sama-sama merupakan bilangan bulat. Tapi, bagaimana jika salah satunya ada yang desimal? Contohnya, 5 pangkat berapa yang hasilnya 2.236? Hayooo…
Nah loh! Bingung, kan?
Oleh sebab itu, logaritma membantu kita untuk menemukan jawabannya.
Sekarang kalian paham kan, kenapa harus mempelajari materi logaritma? Selain itu, perlu kamu ketahui juga nih, materi logaritma ini tidak hanya digunakan di bidang studi matematika saja loh, tapi juga di bidang studi lain, seperti menentukan orde reaksi dalam ilmu laju reaksi kimia, menentukan koefisien serap bunyi dalam ilmu akustik, dan masih banyak lagi. Nyesel nggak sih kalau kamu nggak benar-benar paham dengan materi ini?
Hmmm… benar juga (Sumber: giphy.com)
Sudah tahu belum, di Aplikasi belajar Ruangguru, ada fitur Drill Soal yang berisi kumpulan contoh soal latihan beserta pembahasannya, loh. Pas banget kan buat mempersiapkan diri kamu dalam menghadapi ujian nanti. Yuk, klik banner di bawah ini untuk coba fitur Drill Soal!
Sifat-Sifat Logaritma
Logaritma memiliki beberapa sifat jika dimasukkan dalam bentuk fungsi, seperti tabel di bawah ini.
Logaritma memiliki berbagai sifat yang beragam. Sifat-sifat tersebut akan membantu dalam menyelesaikan soal-soal yang berkaitan dengan logaritma. Berikut sifat-sifat logaritma yang disadur dari laman Kumparan.com.